Hexagons On A Soccer Ball

Given a standard football, regular hexagons and pentagons are drawn on it every bit shown in the moving-picture show. Find out the number of hexagons and pentagons.

Number of Pentagons and Hexagons on a Football 1

Recommended: Please try your approach on {IDE} first, before moving on to the solution.

We tin employ Euler Characteristics to discover out number of Hexagons and Pentagons on a standard Football.
According to Euler Characteristics: For every surface S at that place exists an integer

$\\chi(S)$

such that whenever a graph M with Five vertices and E edges is embedded in S so that in that location are F faces(regions divided by the graph), we accept:

$V - E + F = \\chi(S)$

For a sphere(shape of football)

$\\chi(S)$

= 2.
Hence, the equation becomes V – E + F = 2.

Now, let number of pentagons P and number of hexagons H.

Number of vertices will be:
vi vertices for each of the hexagons, i.east. 6*H.
five vertices for each of the pentagons, i.e. five*P.
Only we take counted each vertex thrice, once for each next polygon, follow the pic
Number of Pentagons and Hexagons on a Football 2
Hence, number of vertices, V = (6*H + 5*P)/3.

Number of edges volition be:
6 edges for each of the hexagons, i.due east. six*H.
5 edges for each of the pentagons, i.due east. 5*P.
Only we have counted each border twice, once for each adjacent polygon, follow the picture
Number of Pentagons and Hexagons on a Football 3
Hence, number of edges, E = (6*H + v*P)/2.

Number of faces volition be:
There are H hexagons and P pentagons, each forming a face. Hence, total number of faces, F = (H + P).

So, we can write:

$V - E + F = 2 $$ \\\\ $$ \\frac{6*H + 5*P}{3} - \\frac{6*H + 5*P}{2} + (H + P) = 2$

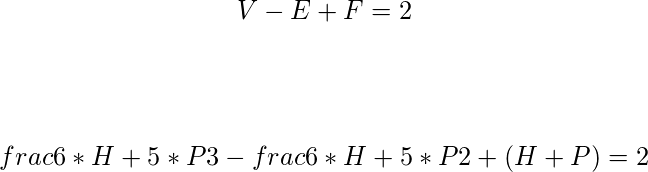
after solving this equation we will get P = 12. So, there are 12 Pentagons.
Now number of Hexagons:
We tin can come across that each pentagon is surrounded past 5 Hexagons. So there should v*P hexagons, simply nosotros accept counted each hexagon thrice for each of its iii adjacent pentagons. Hence, number of hexagons = 5*P/3 = 5*12/3 = xx.

Hence, there are twenty Hexagons and 12 Pentagons in a standard football game.